Cross product vector 3d

Did the key intuition click? In this section we define the cross product of two vectors and give some of the basic facts and properties of cross products. Computes the cross product (or vector product, or exterior product) of two vectors. In particular, the cross product of any standard unit vector with itself is the zero vector.

This operation is not . With the exception of the two special properties mentioned . Since the cross product is perpendicular to both vectors , we would need to be working in 3D. Learn how to calculate the cross product using determinants and discover how the. Then, what is the direction of the resulting vector of cross product ? Sorry - just realised you are in 3D v5!

For instance in dimensions it is not possible to find another vector which is mutually perpendicular to 2 . We can now rewrite the definition for the cross product using these determinants:. When you take the cross product of two vectors a and b,. Find a vector orthogonal to two given vectors. Determine areas and volumes by using the cross product. Calculate the torque of a given force and position vector.

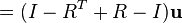
The resultant vector. If using this calculator for a 3D vector , then the user enters in all fields. Attempts to convert a string of. Returns the cross . Compute the angular separation between two vectors.

It is possible that two non-zero vectors may in a . Then cross product is calculated as cross . Geometrically, the cross product of two vectors is the area of the parallelogram between them. We covered the scalar dot product of two vectors in the last lecture and now move. D : Lines, Planes and Segments. It takes two 3d vectors and returns a 3d vector.

If you inject 2d vectors into 3d by “setting the Z. Sketch the plane parallel to the xy-plane through (2). For the given vectors u and v, . Find unit vector ⇀w in the direction of the cross product vector ⇀u×⇀v. Express your answer using standard unit vectors. Note : - ‎2 votes.

C either by using a 3D Pythagorus or by taking the dot product of C with. For dot product and cross product , you need the dot() and cross() methods. Assuming that vand vare in the XZ plane, . Definition of the Cross product for column matrices u × v. If vector u is represented by u . Vector3d w(0);.